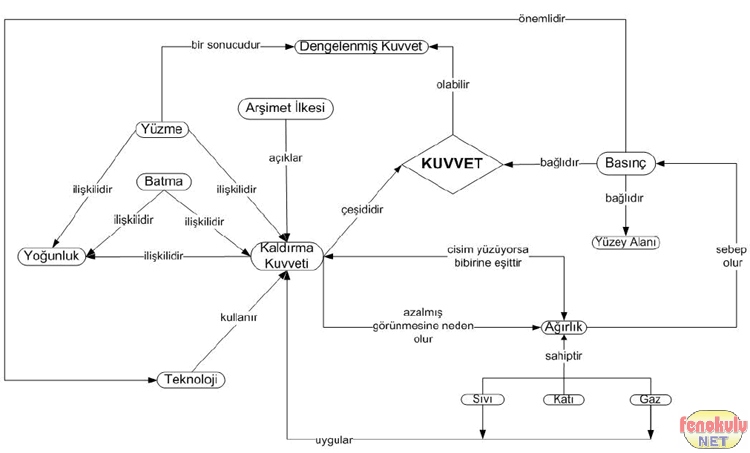
Atmosferi oluşturan gazlar, ağırlıkları ile cisimler üzerine bir kuvvet uygular. Bu kuvvete atmosfer basıncı denir. Atmosfer basıncı barometre ile ölçülür ve milibar(mb) birimi ile değerlendirilir. Normal hava basıncı, 45° enleminde, 15°C sıcaklıkta ve deniz yüzeyinde 1cm² ‘lik yüzeye düşen havanın ağırlığıdır. Bu ağırlık 1033 gr’dır ve 1013 mb hava basıncına eşittir.
1013 milibar normal basınç kabul edilir. Bu değerin üzerindekilere yüksek basınç(antisiklon), altındakilere ise, alçak basınç(siklon) denir. Yeryüzünde şimdiye kadar ölçülmüş en yüksek basınç değeri 1079 mb’dır. Ölçülen en düşük basınç ise 886 mb’dır. Hava basıncı ilk kez 1643 yılında İtalyan bilim adamı Torricelli tarafından civalı bir barometre ile ölçülmüştür. Toriçelli, deneyini deniz seviyesinde 15°C’de yapmıştır. Uzunluğu 1 metre olan ucu kapalı 1 cm çapında cam boru tamamen civa doldurularak açık ağzı kapatılmış ve civa kabına daldırdıktan sonra açılmıştır. Boru içerisindeki civa tamamen kaba boşalmayıp 76 cm’de dengede kaldığı gözlenmiştir. Atmosfer basıncı yere ve zamana göre farklılık gösterir.
Atmosfer basıncını etkileyen faktörler şunlardır;
1. Sıcaklık
Hava ısındıkça genleşir ve hafifler. Soğudukça sıkışır ve ağırlaşır. Bu nedenle havanın soğuk olduğu yerlerde basınç yüksek, sıcak olduğu yerlerde düşüktür. Yani sıcaklıkla basınç arasında ters orantı vardır. Bu yüzden ekvatorda alçak basınç alanı, kutuplarda ise yüksek basınç alanı bulunur.
2. Mevsim
Mevsime göre sıcaklık değiştiği için atmosfer basıncı da değişir. Örneğin; Türkiye’de yaz mevsiminde daha çok alçak basınç alanları, kış mevsiminde ise yüksek basınçalanları oluşur.
3. Yükseklik
Yükselti ile basınç arasında ters orantı vardır. Yükseklere çıkıldıkça atmosferin basıncı düşer. Bunun nedeni yükseldikçe atmosferin kalınlığı ile birlikte ağırlığının ve gazlarının yoğunluğunun azalmasıdır.
4. Yerçekimi
Yerçekimi ile basınç arasında doğru orantı vardır. Yerçekimi arttıkça basınç da artış gösterir. Cisimlerin ağırlığı yerçekimine bağlıdır. Yerçekimi dünyanın şeklinde dolayı ekvatorda az, kutuplarda fazladır. Buna bağlı olarak hava basıncı ekvatorda, kutuplara göre daha azdır.
5. Dinamik Etkenler
Hava kütlelerinin alçalarak yığılması veya yükselerek seyrelmesi sonucunda ortaya çıkar. Örneğin troposferin üst kısımlarında ekvatordan kutuplara doğru esen ters alize rüzgarları dünyanın günlük hareketinin etkisiyle 30° enlemleri civarında alçalarak yüksek basınç alanlarını oluştururlar.
Batı ve kutup rüzgarları ise 60° enlemleri civarında karşılaşıp yükselirler ve burada alçak basınç alanalrını oluştururlar. Bu şekilde hava hareketlerine bağlı olarak oluşan basınç merkezlerine dinamik basınç merkezleri denir.
6. Rüzgarlar
Rüzgarlar havanın yoğunluğunu ve sıcaklığını etkileyerek atmosfer basıncını değiştirir.
Açık Hava Basıncının Ölçülmesi
Açık hava basıncının değeri yeryüzüne yakın yerlerde en büyüktür. Yükseklere çıkıldıkça, hava molekülleri azalacağı için açık hava basıncının değeri azalır.
Toriçelli Deneyi
Yaklaşık bir metre uzunluğun da olan bir ucu kapalı cam boru alınarak ağzına kadar cıva dolduruluyor. Borunun açık kısmı el ile kapatılıp cıva çanağına daldırıldıktan sonra el çekildiğinde, cıvanın biraz çanağa boşalıp sonra sabit kaldığı görülüyor. Bu durumda borudaki cıva yüksekliği 76 cm oluyor.
Borunun ağzı açık olduğu halde cıvanın tamamının çanağa boşalmamasının nedeni, cıva basıncının açık hava basıncı tarafından dengelenmesidir.
Aynı deney farklı genişlikteki borularla yapıldığında cıva düzeyleri arasındaki farkın yine 76 cm olduğu görülüyor. Yani borudaki cıva yüksekliği borunun kesitine bağlı değildir.
Toriçelli bu deneyi deniz seviyesinde ve 0 °C sıcaklıkta yapmıştır.
Açık hava basıncının ölçüldüğü aletlere barometre denir.
Buna göre,
P0 = Pcıva
P0 = h . r = 76 . 13,6
P0 = 1033,6 g.f/cm2 dir.
Bu sonuca göre açık hava, deniz düzeyinde 1 cm2 lik yüzeye 1 kg-f den fazla yani yaklaşık 10 N değerinde kuvvet uygulamaktadır.
Açık hava basıncı (P0): Atmosfer adını verdiğimiz ve kalınlığı kilometreleri bulan hava yerküreyi kuşatmaktadır. Açık hava hem yeryüzüne hem de içerisinde bulunan bütün yüzeylere ağırlığı nedeniyle bir kuvvet uygular. Bu kuvvetin yüzeyin birim alanına düşen kısmına açık hava basıncı yada atmosfer basıncı denir.
Toriçelli deneyi:

Toriçelli 80-90cm uzunluğunda bir cam boru alarak tamamen civa ile doldurmuştur. Daha sonra civa dolu cam boruyu ters çevirerek, içerisinde civa bulunan civa kabına koyduktan sonra burudaki civanın bir kısmının civa kabına boşaldığını ve 76cm yüksekliğini alacak şekilde dengede kaldığını gözlemiştir. Civanın tamamen boşalmamasının sebebi, açık hava basıncının borudaki civa basıncını dengelemesidir. Yani borudaki civa(sıvı) basıncı kaptaki civanın üst yüzeyine etkiyen açık hava basıncına eşittir. Toriçelli bu deneyi değişik kesitteki borularla denemiş ve sonucun değişmediğini gözlemiştir. O halde civa yüksekliği borunun kesitine bağlı değildir. Toriçelli bu deneyi deniz kıyısında ve sıcaklığın 0°C olduğu bir günde yapmıştır.
Civanın özağırlığı 13.6 olduğundan borudaki sıvı basıncı(ki bu basınç açık hava basıncına eşittir);
P0=h×d=1Atm olur.
Açık hava basıncını ölçen aletlere
barometre denir. Barometredeki civa seviyesi her 10.5m yüksekliğe çıkıldıkça 1mm düşer. Bundan yararlanarak rakım ölçülür.turkeyarena.com
Kapalı Kaplardaki Gazların Basıncı: Sıvılar gibi gazlarda içinde bulundukları kabın çeperlerine basınç uygularlar. Bu basınç gaz moleküllerinin hareketinden ileri gelir. Kapalı bir kapta bulunan gaz basıncı;
1. Hacimle ters orantılıdır. Sıcaklık sabit kalmak şartıyla hacim azaldıkça basınç artar.
2. Hacim sabit kalmak şartıyla, sıcaklık arttıkça basınç artar.
3. Molekül sayısı ile doğru orantılıdır. Hacim sabit iken molekül sayısı arttıkça basınç artar.
Bu üç madde ideal gaz denklemi ile ifade edilir;
P.V=n.R.T
P: basınç V: hacim
n: molekül sayısı R: genel gaz sabiti
T: sıcaklık(T=273+t°C)
TORİÇELLİ BORUSU İLE AÇIK HAVA BASINCININ ÖLÇÜLMESİ
DENEYİN AMACI: Açık hava basıncını toriçelli borusu ile ölçmek.
HAZIRLIK SORULARI:
1-Açık hava basıncını nasıl ölçebiliriz? Araştırınız.
2-Toriçelli kimdir? Araştırınız.
KULLANILAN ARAÇ VE GEREÇLER:
1.statif çubuk (100 cm – 2 adet)
2.büyük üç ayak ( 2 adet)
3.civa çanağı ve damlalığı
4.bunzen kıskacı (2 adet)
5.bağlama parçası (2 adet)
6.civa
7.toriçelli borusu
8.plastik küvet
9.metre (en az 100 cm ‘lik)
DENEYİN YAPILIŞI:
1-Civa çanağı haznesinin yarısına kadar civa doldurunuz.
2-Toriçelli borusuna civa damlalığı ile civa doldurunuz. İşaret parmağınızın ucuyla borunun ağzını kapatıp ters çeviriniz. Civa çanağına hava kaçmayacak şekilde daldırıp, parmağınızı çekiniz.
3-Toriçelli borusunu şekildeki gibi Bunzen kıskacıyla Statif çubuğa sabitleyiniz.turkeyarena.com
4-Metreyi Statif çubuğa tutturarak civa yüksekliğini ölçünüz.
DENEYİN SONUCU:
Bu deneyde civa basıncı açık hava basıncı ile dengelenerek, AHB’nin değeri ölçülmüştür. Laboratuvar koşullarında ölçtüğünüz değer 76 cm olmayabilir.
NOT:Civa buharı zehirlidir. Ayrıca altınla çok şiddetli reaksiyon verdiği için, çalışmalarınızda takı bulundurulması sakıncalıdır.
TEORİK BİLGİ:
Toriçelli açık hava basıncını, sıvı basıncından faydalanarak hesaplamayı başarmıştır. Toriçelli deneyi; deniz seviyesinde ve sıcaklığın 0 0C olduğu bir günde yapılırsa, içi civa dolu 1 metrelik bir ucu açık cam borunun civa yüksekliğinin 76 cm ‘ye düştüğü görülür. Buna normal hava basıncı denir.
Açık hava basıncının değeri yeryüzüne yakın yerlerde en büyüktür. Yükseklere çıkıldıkça hava molekülleri azalacağından açık hava basıncının değeri düşer.
Açık Hava Basıncının Etkileri

İçi su dolu bardağın ağzı hava kalmayacak şekilde kağıtla kapatılıp şekildeki gibi ters çevrildiğinde suyun dökülmediği görülür. Suyun dökülmemesinin nedeni, suyun kağıda uyguladığı basıncın, açık havanın kağıda uyguladığı basınca eşit ya da küçük olmasıdır.
- Bir yerden başka bir yere uygun şartlarda akabilen maddelere akışkan maddeler denir. Sıvılar ve gazlar akışkan maddelere örnektir.
- Akışkanlar daima basıncın büyük olduğu yerden küçük olduğu yöne doğru akar. Dağlarda da sular daima aşağı doğru akar. Binaların zeminindeki strofor yardımı ile basınç farkı oluşturularak, su binanın üst katlarına kadar çıkarılır. Odanın kapı ve penceresini açarak hava akımı oluşturulması da basınç farkından dolayıdır.
- Yükseğe yerleştirilmiş bir depoya şekildeki gibi üstten bir hortum daldırılıp, hortumun içindeki havayı boşaltırsak depodaki sıvıyı akmaya zorlarız. Eğer borunun içindeki hava boşaltılıp borunun ağız hizası, suyun üst düzeyinden aşağıda olmaz ise sıvı akışı başlamaz. Akmaya başladıktan sonra depodaki sıvı bitinceye kadar akma devam eder. Sistem yine hız ile basınç arasındaki ters orantıdan yararlanılarak çalıştırılır. Suyun L noktasındaki hızı K noktasındaki hızından büyük olacağından, L noktasında sıvı basıncı düşer, böylece su devamlı akmış olur. Böcek ilaçlamaya yarayan filit pompanın çalışması da aynı ilkelere dayanır.
- Musluktan akan suyun aşağı doğru hızı artar ve kesiti daralarak incelir.





























 çekimi ivmesi bilinmelidir.
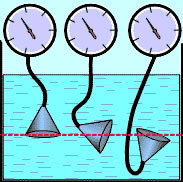
çekimi ivmesi bilinmelidir. Sıvı Basıncına Derinliğin Etkisi
Sıvı Basıncına Derinliğin Etkisi
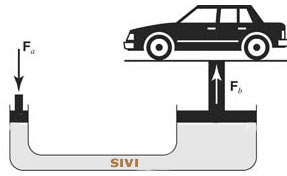 Yandaki resim otomobil tamirhanelerinde araçları kaldırmak için uygulanan bir yöntemi gösteriyor. Pascal Prensibine göre çalışan bu kaldıraçta küçük pistondan uygulanan kuvvet (Fa) sıvıya iletilmekte, sıvı da bu basıncı doğrudan diğer pistona ileterek arabanın havaya kalkmasını sağlamaktadır.
Yandaki resim otomobil tamirhanelerinde araçları kaldırmak için uygulanan bir yöntemi gösteriyor. Pascal Prensibine göre çalışan bu kaldıraçta küçük pistondan uygulanan kuvvet (Fa) sıvıya iletilmekte, sıvı da bu basıncı doğrudan diğer pistona ileterek arabanın havaya kalkmasını sağlamaktadır.